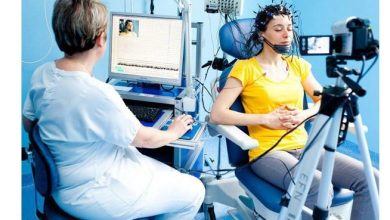
الکتروآنسفالوگرام چیست؟-بخش دوم
استخراج ویژگی
آنالیز سری های زمانی اغلب با استخراج ویژگی از سیگنال مورد نظر انجام می شود. ویژگی ها می توانند به عنوان پارامترهایی تعریف شوند که حاوی اطلاعاتی در مورد ساختار سیگنال مورد بررسی هستند. روش های زیادی برای استخراج ویژگی از سیگنال ها وجود دارد. باید توجه داشت که در حالت کلی، برای مطالعه سیگنال ها و شناسایی پدیده های مختلف، از چندین ویژگی استفاده میشود چراکه ویژگی های مختلف میتوانند مکمل یکدیگر بوده و به استخدام در آوردن همزمان تعدادی از آنها با هم می تواند منجر به نتایج مطلوبتری شود.
پردازش در حوزه زمان
ویژگی های زمانی، دستهای از ویژگی ها هستند که از سیگنال در حوزه زمان استخراج میشوند. این ویژگی ها، حاوی اطلاعاتی در حوزه زمان بوده و معمولاً به سادگی قابل محاسبه و استخراج هستند. این ویژگی ها معمولاً به ازای یک پنجره زمانی از سیگنال اصلی محاسبه می شوند. با توجه به اینکه سیگنال در حوزه زمان، در حقیقت، به معنای تغییرات دامنه برحسب زمان است، ویژگی های حوزه زمان بخش محدودی از اطلاعات مفید سیگنال را استخراج خواهند کرد و لازم است تا ویژگی های مربوط به حوزههای دیگر مانند حوزه فرکانس و یا تبدیل موجک نیز در نظر گرفته شود.
پردازش در حوزه فرکانس
یکی از راه های مرسوم برای دستیابی به بخشی از اطلاعات موجود در سیگنال تغییر حوزه اطلاعاتی سیگنال است. حوزه فرکانس به عنوان یکی از مرسوم ترین حوزه ها، به منظور استخراج ویژگی مورد توجه است. طبق تعریف تبدیل فوریه زمان پیوسته سیگنال پیوسته و همچنین معکوس آن، مطابق با فرمول (۲) و (۳) به دست میآید.
معرف فرکانس و معرف زمان است. سیگنال اصلی را در حوزه فرکانس بیان میکند. حاوی اطلاعات مفیدی خواهد بود که در حوزه زمان قابل مشاهده نیست. ویژگی های مختلفی که از حوزه فرکانس یک سیگنال به دست میآید در آنالیز و شناسایی الگوها بسیار مفید خواهد بود.
ملاحظه میشود که در رابطه (۲) حدود انتگرال از تا است. نامحدود بودن حدود انتگرالگ یری بیانگر بیاهمیت بودن زمان حضور مؤلفه در سیگنال است. به بیان دیگر، در تبدیل فوریه، مؤلفه فرکانسی هر جای سیگنال که باشد، با انتگرال گیری از تا شناسایی خواهد شد. در رابطه تبدیل فوریه در حقیقت میزان شباهت بین و محاسبه شده است. این شباهت سنجی به ازای یک فرکانس خاص در همه زمان ها محاسبه میشود. از طرفی می توان دریافت که تبدیل فوریه قابلیت تشخیص زمان حضور یک فرکانس خاص در سیگنال را ندارد، و این یعنی نداشتن حساسیت و رزولوشن نسبت به زمان. این موضوع یک عیب برای تبدیل فوریه خواهد بود، زیرا بخشی از اطلاعات مفید سیگنال مربوط به مؤلفه های فرکانسی خاصی است که در بازه زمانی کوتاهی آشکار میشوند. تبدیل فوریه توانایی تعقیب این تغییرات سریع را ندارد. یکی از ابزارهای بسیار مفید برای برطرف کردن این عیب تبدیل موجک است.
پردازش در حوزه موجک
تبدیل موجک[۱] (WT) یکی از ابزارهای بسیار مفید برای آنالیز زمان- فرکانسی سیگنال است. در تبدیل موجک کرنل زمان- فرکانس به گونه ای است که مؤلفه های زمان و فرکانس موجود در سیگنال را به خوبی تشخیص داده و استخراج میکند
تبدیل موجک گسسته
برای پردازش سیگنال های دیجیتال یک تقریب گسسته از ضرایب موجک نیاز است. در صورتی که سیگنال مورد بررسی در یک باند فرکانسی محدود قرار داشته باشد، تبدیل موجک گسسته[۲] (DWT) میتواند براساس تئوری نمونه برداری استخراج شود.
نسخه پیوسته WT میتواند با ملاحظات ساده ای نسبت به تغییر الگوی موجک بر اثر تأخیر گسسته سازی شود. از آنجا که در حالت کلی تابع موجک محدود به باند فرکانسی خاصی نیست، به منظور جلوگیری از پدیده الیاسینگ (همپوشانی فرکانسی)[۳]، لازم است تا بخشی از مؤلفه های فرکانسی تابع موجک سرکوب یا حذف شوند. مؤلفه های سرکوب شده دارای فرکانسی بیش از نصف فرکانس نمونه برداری می باشند.
فضای فوریه می تواند به منظور محاسبه تبدیل موجک در مقیاس های مختلف مورد استفاده قرار گیرد. در صورتی که پهنای باند فرکانسی کاهش یابد، تعداد المانها برای یک مقیاس خاص نیز کاهش خواهد یافت. یک تجزیه از سیگنال اطلاعات بسیار مفیدی در مورد کاهش المانها در هر مقیاس به دست میدهد. این تجزیه در هر گام، باند فرکانسی سیگنال را به دو بخش تقسیم میکند. موجک مربوطه به خوبی در فضای فوریه محلی سازی شده است. این محلی بودن قابلیت دسته ای از آنالیزها را میدهد که در فضای اصلی امکانپذیر نیست.
تقسیم بندی به دو بخش در هر گام از تجزیه امکان بررسی اتفاقات در مقیاس های مختلف را فراهم میکند. به این ترتیب که در گام های نخست مقیاس تابع موجک بزرگ بوده و میتواند الگوها و رخدادهایی را که در بازههای زمانی بلند در سیگنال اتفاق افتاده است شناسایی کند. در گام های بعدی با نصف شدن مقیاس تابع موجک، به تدریج امکان بررسی الگوها و رخدادهایی که در بازه های زمانی کوتاه اتفاق میافتد فراهم میشود. این قابلیت، همانطور که پیشتر ذکر شد، مانند یک میکروسکوپ ریاضیاتی عمل خواهد کرد. این میکروسکوپ نسبت به میزان بزرگی، سرعت و یا دینامیک رخداد حساسیتی ندارد چراکه میان تابع موجک و سیگنال اصلی، به ازای مقیاسهای مختلف تابع موجک، شباهتسنجی کرده و تمام دینامیکها را شناسایی میکند.
از یک منظر دیگر که نتایج بسیار کاربردی در خصوص پردازش سیگنال ها به دست میدهد، تقسیم بندی دو بخشی تابع اصلی یا سیگنال مورد بررسی را میتوان به صورت یک فیلتر پایین گذر و یک فیلتر بالاگذر تحلیل کرد. به این ترتیب در هر گام از تجزیه، سیگنال به دو بخش تقسیم میشود که یک بخش حاوی اطلاعات فرکانس پایین و یک بخش حاوی اطلاعات فرکانس بالای سیگنال است. اطلاعات فرکانس پایین در حقیقت مربوط به یک تقریب[۴] (A) از سیگنال هستند. بخش تقریب رفتارهای کلی یا دینامیک های با سرعت پایین سیگنال را نشان میدهد. اطلاعات فرکانس بالا در حقیقت مربوط به جزئیات[۵] (D) سیگنال هستند. بخش جزئیات رفتارهای جزئی یا دینامیک های با سرعت بالای سیگنال را نشان میدهد. برای مثال، اگر سیگنال اصلی دارای باند فرکانسی Hz 256-0 است، بخش A باند فرکانسی Hz 128-0 و بخش D باند فرکانسی Hz 256-128 را به خود اختصاص خواهد داد. در گام بعدی، بخش A، مانند گام قبل، به دو بخش A1 (Hz 64-0) و D1 (Hz 128-64) تقسیم میشود. به همین ترتیب، با توجه به دانش ابتدایی نسبت به الگوهای مورد نظر در سیگنال اصلی، تا هر تعداد گام که لازم باشد میتوان جلو رفت.
انتخاب ویژگی
ویژگی، خصیصه قابل اندازه گیری منحصر به فرد در فرآیند مشاهده شده است. با استفاده از مجموعه ای از ویژگی ها یک الگوریتم بینایی ماشین یا شناسایی الگو، قادر به انجام کلاس بندی خواهد بود. در سال های اخیر در کاربردهای بینایی ماشین و یا شناسایی الگو دامنه ویژگی ها تا چند هزار متغیر یا ویژگی گسترش پیدا کرده است. تکنیک های متعددی برای حل مسئله کاهش متغیرهای غیرمرتبط و متغیرهای دچار افزونگی[۶]، که چالش اصلی در این مسائل هستند، ایجاد شده است. انتخاب ویژگی (حذف متغیر) به فهم داده ها، کاهش محاسبات مورد نیاز، کاهش اثر نفرین بُعد[۷] و بهبود عملکرد پیشبینی کننده کمک میکند. در بسیاری از کاربردهای عملی برای استخراج ویژگیها از سنسورها و یا الکترودها استفاده میشود. با به کارگیری روش های انتخاب ویژگی، کاهش هوشمندانه تعداد ویژگی ها، تعداد سنسورها و یا الکترودهای ثبت را کاهش خواهد داد. به این ترتیب هزینه های عملیاتی برای پردازش سیگنالها و اطلاعات مورد نظر کاهش خواهد یافت.
تمرکز بر روی انتخاب ویژگی به معنی انتخاب یک زیرمجموعه از متغیرهای ورودی است، به نحوی که بتواند به طور مؤثر دادههای ورودی را توصیف کرده و در عین حال اثرات ناشی از نویز یا متغیرهای غیرمرتبط را کاهش دهد. این زیرمجموعه همچنین باید قادر باشد نتایج قابل قبول پیشبینی کننده (کلاس بند) را حفظ کند.
متغیرهای وابسته به هم در بردارنده هیچ اطلاعات جدیدی در مورد کلاس ها نیستند، به همین خاطر به عنوان نویز برای کلاس بند مطرح می شوند. این وابستگی نشان می دهد که اطلاعات مفید، به طور کامل، میتواند از میان تعداد کمتری ویژگی های یکتا استخراج شده و در عین حال بیشترین جدایی اطلاعات را در مورد کلاس ها به همراه داشته باشد. در نتیجه، با حذف متغیرهای وابسته مقدار دادهها کاهش خواهد یافت و این کاهش مقدار داده ها می تواند منجر به بهبود عملکرد کلاس بند شود. در برخی کاربردها، متغیرهایی که هیچ همبستگی[۸] نسبت به کلاس ها ندارند به عنوان نویز در نظر گرفته می شوند و ممکن است بایاسی را به کلاس بند تحمیل کرده و عملکرد کلاس بند را تضعیف کنند. این موضوع میتواند در مواردی که اطلاعات پیرامون فرآیند مورد مطالعه کم است رخ دهد. با اعمال روش های انتخاب ویژگی می توان بینش و درونبینی عمیقتری نسبت به فرآیند پیدا کرده و محاسبات مورد نیاز را کاهش و صحت کلاس بند را بهبود داد.
برای حذف ویژگی های غیرمرتبط، یک معیار انتخاب ویژگی نیاز است. این معیار باید بتواند میزان ارتباط هر ویژگی با کلاس یا برچسب خروجی را به صورت کمّی ارزیابی نماید. از دیدگاه بینایی ماشین، اگر یک سیستم از متغیرهای غیرمرتبط استفاده نماید، آنگاه استفاده از اطلاعات مربوط به این متغیرها برای دادههای جدید منجر به تضعیف تعمیم پذیری[۹] سیستم میشود. حذف متغیرهای غیرمرتبط نباید با روشهای دیگر کاهش بُعد مانند آنالیز مؤلفههای اساسی[۱۰] (PCA) مقایسه شود، زیرا ویژگی های مناسب میتواند مستقل از باقیمانده داده ها باشد. حذف ویژگی، ویژگی جدیدی تولید نمیکند، بلکه ویژگی های استخراج شده را در ورودی گرفته و تعداد آنها را کاهش میدهد. وقتی معیار ارزیابی برای انتخاب ویژگی تعیین شد، طی یک فرآیند، زیرمجموعه ای از ویژگیهای مفید جست و جو و انتخاب خواهد شد. ارزیابی مستقیم همه زیرمجموعه های قابل انتخاب از ویژگیها (N2) برای دادههای موجود، با افزایش تعداد ویژگیها، یقیناً به لحاظ محاسباتی بسیار طولانی و دچار نفرین بُعد خواهد شد. به همین خاطر لازم است تا یک فرآیند زیربهینه[۱۱] به کار گرفته شود به طوری که هم بتوان دادهه ای با افزونگی را حذف کرد و هم بتوان محاسبات مربوطه را کاهش داد.
مراجع
Andreassi, JL. “Psychophysiology: Human Behaviour & Physiological Response” London: Lawrence Erlbaum Associates, 2000.Stern, W. Ray and K. Quigley, “Psychophysiological Recording” Oxford: Oxford University Press, 2001.
- Hyvärinen “Independent component analysis: recent advances” Phil Trans R Soc A 371: 20110534, 2013.
- Sanei and J. A. Chambers. “EEG Signal Processing” ۲۰۰۷٫
- E. Cherry, “Some experiments in the recognition of speech, with one and two ears” J. Acoust. Soc. Am., 25: 975–۹۷۹, ۱۹۵۳٫
- Herault, and C. Jutten, “Space or time adaptive signal processing by neural models” Proceeding of the American Institute of Physics (AIP) Conference on Neural Networks for Computing, pp. 206–۲۱۱, ۱۹۸۶٫
- Comon, “Independent component analysis: a new concept” Signal Process., 36: 287–۳۱۴, ۱۹۹۴٫
- P. Jung, S. Makeig, C. Humphries, T. W. Lee, M. J. McKeown, V. Iragui and T. J. Sejnowski, “Removing electroencephalographic artefacts by blind source separation” Psychophysiology, 37: 163–۱۷۸, ۲۰۰۰٫
- Shoker, S. Sanei, and J. Chambers, “Artifact removal from electroencephalograms using a hybrid BSS-SVM algorithm” IEEE Signal Process. Lett., 12(10), October 2005.
- Shoker, S. Sanei, and J. Chambers, “A hybrid algorithm for the removal of eye blinking artefacts from electroencephalograms” in Proceedings of the IEEE Statistical Signal Processing Workshop, France, SSP2005, February 2005.
- Corsini, L. Shoker, S. Sanei, and G. Alarcon, “Epileptic seizure prediction from scalp EEG incorporating BSS” IEEE Trans. Biomed. Eng., 53(5): 790–۷۹۹, May 2006.
- A. Latif, S. Sanei, and J. Chambers, “Localization of abnormal EEG sources blind source separation partially constrained by the locations of known sources” IEEE Signal Process, Lett., 13(3): 117–۱۲۰, March 2006.
- Spyrou, M. Jing, S. Sanei, and A. Sumich, “Separation and localisation of P300 sources and the subcomponents using constrained blind source separation” EURASIP J. Adv. Signal Process., Article ID 82912, November 2006.
- Hyvärinen and E. Oja, “Independent component analysis: algorithms and applications” Journal of Neural Networks, 13: 411–۴۳۰, ۲۰۰۰٫
- Hyvärinen, “Fast and robust fixed-point algorithms for independent component analysis” IEEE Transactions on Neural Networks, 10 (3): 626–۶۳۴, ۱۹۹۹٫
- Murenzi, J. M. Combes, A. Grossman, and P. Tchmitchian, (Eds), Wavelets, Springer-Verlag, Berlin, Heidelberg, New York, 1988.
- J. Franaszczuk, G. K. Bergey, and P. J. Durka, “Time–frequency analysis of mesial temporal lobe seizures using the matching pursuit algorithm” Soc. Neurosci. Abstr., 22: 184, 1996.
- Holschneider, R. Kronland-Martinet, J. Morlet, and Ph. Tchamitchian, “A real-time algorithm for signal analysis with the help of the wavelet transform” in Wavelets: Time–Frequency Methods and Phase Space, Eds J. M. Combes, A. Grossman, and Ph. Tchamitchian, Springer-Verlag, Berlin, pp. 286–۲۹۷, ۱۹۸۹٫
- Murenzi, J. M. Combes, A. Grossman, and P. Tchmitchian, (Eds), Wavelets, Springer-Verlag, Berlin, Heidelberg, New York, 1988.
- Guyon, A. Elisseeff, “An introduction to variable and feature selection” J Mach Learn Res, 3:1157–۸۲, ۲۰۰۳٫
- Alpaydin “Introduction to machine learning” The MIT Press; 2004.
MH Law, M rio AT Figueiredo, AK Jain, “Simultaneous feature selection and clustering using mixture models” IEEE Trans Pattern Anal Mach Intell, 26, 2004.
- Kohavi, GH. John “Wrappers for feature subset selection” Artif Intell, 97:273–۳۲۴, ۱۹۹۷٫
- Yang, H. Yoon, C. Shahabi, “A supervised feature subset selection technique for multivariate time series” in: Workshop Feature Selection for Data Mining: Interfacing Machine Learning with Statistics, pp. 92–۱۰۱, ۲۰۰۵٫
- Javed, H. Babri and M. Saeed, “Feature selection based on class-dependent densities for high-dimensional binary data” IEEE Trans, Knowl, Data Eng, 24: 465–۴۷۷, ۲۰۱۲٫
- M. Sotoca and F. Pla, “Supervised feature selection by clustering using conditional mutual information-based distances” Patt. Recog, 43: 2068–۲۰۸۱, ۲۰۱۰٫
- Cheema, T. Henne, U. Koeckemann and E. Prassler, “Applicability of feature selection on multivariate time series data for robotic discovery” in: 3rd International Conference on Advanced Computer Theory and Engineering (ICACTE ‘۱۰), pp. V2-592-V592-597, 2010.
M.W. Kadous, “Temporal classification: extending the classification paradigm to multivariate time series” Doctoral Dissertation, School of Computer Science and Engineering, The University of New South Wales, 2002.
- Shahabi, “AIMS: an immersidata management system, in: VLDB First Biennial Conference on Innovative Data Systems Research” (CIDR ‘۰۳), ۲۰۰۳٫
- Tanawongsuwan, A. Bobick, “Performance analysis of time-distance gait parameters under different speeds” in: 4th International Conference on Audio- and Video-based Biometric Person Authentication (AVBPA ‘۰۳) Springer, pp. 715–۷۲۴, ۲۰۰۳٫
- Brown, A. Pocock, M.J. Zhao and M. Luja´n, “Conditional likelihood maximisation: a unifying framework for information theoretic feature selection” J. Mach, Learn. Res, 13: 26–۶۶, ۲۰۱۲٫
[۱] Wavelet Transform
[۲] Discrete Wavelet Transform
[۳] Aliasing
[۴] Approximation
[۵] Details
[۶] Redundancy
[۷] Curse of Dimensionality
[۸] Correlation
[۹] Generalization
[۱۰] Principle Component Analysis
[۱۱] Suboptimal
[۱۲] Wrapper